Learning to Dequantise with Truncated Flows
A pet idea that I’ve been coming back to time and again is doing autoregressive language modelling with ``stochastic embeddings’’. Each word would have a distribution over the embedding that represented it, instead of a deterministic embedding. The thought would be that modelling word embeddings in this way would better represent the ability for word meanings to overlap while not completely subsuming the other, or in some cases have multi-modal representations because of the distinct word senses in which they are used (‘bank’ to refer to the ‘land alongside a body of water’ or ‘a financial institution’).
We repeatedly ran into the problem of the posterior collapsing, likely due to the way the encoder and decoder were parameterised.
Categorical Normalising Flows (CatNF) alleviates this problem by defining the decoder as the posterior of the encoder: $$ \begin{align*} p(x_t|z_t) \triangleq \frac{ q(z_t|x_t)~\tilde{p}(x_t)}{ \sum_{x_t'=0}^{K-1}q(z_t|x_t’)~\tilde{p}(x_t’)} \end{align*} $$ This means, with respect to the encoder, the decoder is making the optimal decoding of $z_t$. Graphically:
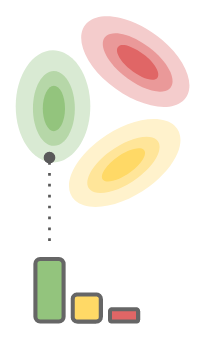
The upshot of this parameterisation is that maximising $\log p(x_t|z_t)$ (which is part of the ELBO loss) will naturally encourage $q(z_t|x_t)$ to be distinct for each category — less posterior collapse!
That was a long setup about CatNF, I thought this was about TRUFL?
TRUFL was positioned as a trade-off between CatNF and Argmax Flow. With CatNF’s framing of the optimal decoder, we can take a look at how they’re related.
First of all, it’s important to note that there are two versions of Argmax Flow presented in their paper. One version requires $z$ to have the same number of dimensions as there are categories $|V|$. The second, which is the version that is implemented in their experiments requires a binary encoding of each category $c \in V$. This allows the dimensionality of $z$ to be $\lceil\log_2 |V|\rceil$.
For example, for 3 categories, we can represent it in 2 dimensions.
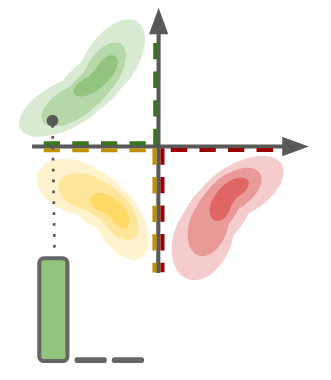
The dotted line represents the support for each category, colour coded accordingly.
- In Argmax Flow, the support for each category are non-overlapping, which allows for deterministic decoding always (consider the posterior for such an encoder with limited support for each category).
- Note how the space is partitioned according to the quadrants. This partitioning is dictated by the binary encoding of $c$, and can be very arbitrary. The parameters for each category can transform the individual $q(z|x)$'s, but ultimately, they are stuck within the pre-specified partitioning.
For TRUFL, we use the idea of limited support for parameterising the distributions in CatNF, which allows for deterministic decoding if the component’s support doesn’t overlap with any other category, while still being able to learn said support.
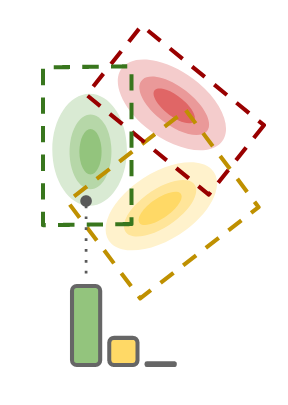
You can do this differentiably?
(I actually looked up if differentiably is a word. Seems like it is.)
Yes. But instead of presenting it how I did in the paper, I’d like to walk this through from a ``normalising flow perspective’’. Let’s start with the Gaussian distribution and the reparameterisation trick: $$z = \mu(x) + \sigma(x) \cdot z_0 \qquad z_0 \sim \mathcal{N}(0,1)$$ If you’re familiar with normalising flows, you already know the reparameterisation trick is simply a shift-scale transform on the random variable $z_0$. Compute the appropriate log det jacobian, and you’re good to go.
We can go further down the rabbit hole and ask: “But where do $z_0$s come from?”
You see when an $\epsilon$ and a $\gamma$ love each other very much-
We can do this: $$z_0 = F^{-1}(u) \qquad u \sim \mathrm{Uniform(0, 1)} \qquad F^{-1}(u) = {\sqrt {2}}\operatorname {erf} ^{-1}(2u-1)$$
$F^{-1}$ is of course the inverse CDF of the normal distribution. This idea is fairly general — any time you have a tractable inverse CDF, you can transform $\mathrm{Uniform}(0,1)$ into that distribution. The log det jacobian is simply the PDF.
To truncate: simply sample $u \sim \mathrm{Uniform}(a(x), b(x))$, while ensuring $(a(x), b(x))$ is an interval in $(0, 1)$: $$u = a(x) + (b(x) - a(x)) \cdot u_0 \qquad u_0 \sim \mathrm{Uniform}(0, 1)$$
So, if $a$ and $b$ are parameterised differentiably, and $F^{-1}$ is differentiable and tractable, this can be used within your network easily as a drop-in replacement, with an additional 2 parameters for the truncation boundaries. In our paper, we use the Logistic distribution as our base distribution, which gives us convenient cumulative (sigmoid) and inverse cumulative (logit) functions.
GIFs please!
Here are some initial animations I wrote up to look at the training dynamics of a CatNF method versus TRUFL. We weigh the reconstruction loss with a 10:1 ratio against the KL term, so that the optimisation prioritises minimising the reconstruction loss.
Understandably, there is no way use a mixture of Logistic distributions to fit a single Logistic distribution without having both components be equal to the prior, i.e. posterior collapse. Since we forced the components to be more distinct via the heavy weight on the reconstruction loss, the loss is suboptimal.
Because of the way TRUFL can learn the support, it can learn to truncate exact halves of the logistic distribution, thereby allowing (nearly) deterministic decoding (in this particular case), but still optimally minimising the KL term. Note the oscillating behaviour at the end there. There are multiple solutions to perform this partitioning, so this is expected.
But it doesn’t do exact partitioning right?
Nope. There are ‘islands’ of support in the latent space, while there are ‘oceans’ of unsupported regions. In the paper, we explore a way of sampling from the model distribution $p(x)$ so that we reject any latent samples that fall into the ‘ocean’.
There has, however, been a more recent development: Voronoi dequantisation Ricky Chen and team use differentiable voronoi partitioning to ensure that the bounded latent space is exactly partitioned into non-overlapping components. This means decoding is deterministic and the locations of each component can be learned.
And that’s it! Hopefully you’ve benefitted from reading this post as much as I’ve learned from working on this project.
@misc{tan2022-04-08,
title = {Learning to Dequantise with Truncated Flows},
author = {Tan, Shawn},
howpublished = {\url{https://blog.wtf.sg/posts/2022-04-08-learning-to-dequantise-with-truncated-flows/}},
year = {2022}
}